Short aside about why this topic was chosen
As I mentioned in my last post, I want to detail things that tend to have poor expositions or poor mathematical rigor. A lot of the mathematical topics I included in my initial schedule are really well exposited in books such as Allen Hatcher’s Algebraic Topology and Differential Forms in Algebraic Topology by Raoul Bott and Loring Tu. These books provide a beautiful combination of geometry, topology and imagery so that the reader has a well-rounded understanding of the topics they are dealing with. I initially wanted to write about these various topics in the blog for my own benefit, but I realized that I would end up rewriting what they have in less clear terms. Instead, I figure that it will be better to focus on objects, dynamical systems and theorems in physics which have poor mathematical descriptions. For example, the classical Bosonic String tends to have two disjoint mathematical and physical descriptions, which are unified to some extent in a few books (e.g. M. Schottenlohen’s A Mathematical Introduction to Conformal Field Theory). I hope to write this article in three parts, emphasizing the intuition in the beginning and the rigor toward the end. I’m going to put the list of references used at the beginning of each article, because it will help those who are more mathematically and/or physically inclined choose what they would like to read.
References
Note 1: I’m going to update the references with all of the ones I used later today (Monday, August 16)
Note 2: If anyone knows of something that will let me use BibTeX in WordPress please, please e-mail me!
[1] Becker, Katrin, Melanie Becker, and John Schwarz. String Theory and M-Theory: A Modern Introduction. 1st. New York: Cambridge University Press, 2007. Print.
[2] Polchinski, Joseph. String Theory. 2nd. 1. New York: Cambridge University Press, 2005. Print.
[3] Schottenloher, Martin. A Mathematical Introduction to Conformal Field Theory. 2nd. Heidelberg: Springer-Verlag, 2008. Print.
[4] Schwarz, John. “A Brief History of Superstrings.” A Brief History of Superstings [sic]. Caltech, n.d. Web. 15 Aug 2010. <http://www.theory.caltech.edu/people/jhs/strings/string13.html>.
[5] Zwiebach, Barton. A First Course in String Theory. 2nd. Cambridge: Cambridge University Press, 2004. Print
Background
Some exposure to the concepts involved in the theories of the following keywords: differential equations, manifolds (esp. the concept of a submanifold and the associated submersions and embeddings), group actions, electromagnetism (necessarily relativistic), Lagrangian mechanics. The history section will be written with the expertise of a mathematician or even an engineering, with some of the rudimentary physical concepts laid out explicitly. The representation theory of the Virasoro algebra will probably be avoided, pending time constraints. However, I may go into how one can mathematically arrive at the algebra via a short-exact sequence called a central extension.
History
Note: The majority of this history is quite basic and general in order to provide any reader with an accessible introduction into the motivation of string theory. Those with quantum mechanics or QFT experience can skip to the section entitled “Development of the String”
String Theory generally finds it’s roots in the 1970s with the ambiguity over the discovery of the strong nuclear force. I’m going to suppose that most people who vaguely pay attention to science news or read popular science magazines know that physicists believe that there are only four forces of nature, namely :
- Electromagnetic Force (EMF)
- Gravity
- Strong (Nuclear) Force
- Weak (Nuclear) Force
The standard presentation of these forces tends to be along the lines of “gravity and EMF are obvious” and the strong and weak forces take too much time to explain, so just accept their existence. While I agree with the first point about gravity and EMF, I figure it would be wise to go through a brief view of the nature of the strong and weak forces as well as experimental evidence.
Weak Nuclear Force
The weak nuclear force has it’s roots in the statistical mechanics studies of Enrico Fermi in the 1930s. The notion of radioactivity has well-defined intuitive and macroscopic meanings, but after the advent of Quantum Mechanics, theoretical physicists were in search of an atomic or subatomic explanation of known macroscopic phenomena. Radioactivity as a macroscopic phenomenon, has its theoretical roots in the radiation theory of classical EMFs. In a sentence, one can define radiation as the emittance of an EMF due to the motion of a particle; examples of radiation range from the benign (your car stereo’s radio) to the malignant (X-Rays,  -Rays). However the treatment of the electron and photon in classical EMF theory assumes that the energy contained within these emitted EMFs continuously change with regard to properties of the distinct particle. The uncertainty principle of Quantum Mechanics, however, makes such labeling of particles as distinct a dubious proposition. Satyendra N. Bose (with later generalization due to Einstein) indirectly gave credence to those who challenged radiative explanations, by showing that the energy distribution of a certain group of particles (now called Bosons) matches experiment if one assumes the particles are indistinguishable (i.e. can’t be labelled individually). Note that the concept of indistinguishable particles is manifestly a quantum mechanical observation; Bose made the discovery while considering the failure of the ultraviolet catastrophe and the effect this has on radiation. While Bose and Einstein didn’t realize it at the time, their discovery provided credence to quantum mechanics in the form of spin. The existence of spin is due to the Stern-Gerlach Experiment, which showed that an electron beam splits into two groups under the influence of a strong magnetic field. Quantum Mechanics was able to absorb this experiment by subsuming a new quantity that behaved (at least algebraically) like angular momentum. Initially, Bose only described the statistics for the photon while Einstein generalized it to certain other components in an atom (e.g. Protons, Neutrons). These components all share one quantifiable quantity: They have integer spin! Putting it all together, we have: The Bose-Einstein Statistics, the distribution of the expected number of bosons at a given energy, describe the energetics of Bosons, or particles with spin
-Rays). However the treatment of the electron and photon in classical EMF theory assumes that the energy contained within these emitted EMFs continuously change with regard to properties of the distinct particle. The uncertainty principle of Quantum Mechanics, however, makes such labeling of particles as distinct a dubious proposition. Satyendra N. Bose (with later generalization due to Einstein) indirectly gave credence to those who challenged radiative explanations, by showing that the energy distribution of a certain group of particles (now called Bosons) matches experiment if one assumes the particles are indistinguishable (i.e. can’t be labelled individually). Note that the concept of indistinguishable particles is manifestly a quantum mechanical observation; Bose made the discovery while considering the failure of the ultraviolet catastrophe and the effect this has on radiation. While Bose and Einstein didn’t realize it at the time, their discovery provided credence to quantum mechanics in the form of spin. The existence of spin is due to the Stern-Gerlach Experiment, which showed that an electron beam splits into two groups under the influence of a strong magnetic field. Quantum Mechanics was able to absorb this experiment by subsuming a new quantity that behaved (at least algebraically) like angular momentum. Initially, Bose only described the statistics for the photon while Einstein generalized it to certain other components in an atom (e.g. Protons, Neutrons). These components all share one quantifiable quantity: They have integer spin! Putting it all together, we have: The Bose-Einstein Statistics, the distribution of the expected number of bosons at a given energy, describe the energetics of Bosons, or particles with spin  .
.
Now back to Fermi: A major contribution of his in the early part of the 1900s was the detailing of the energy distribution for a single particle with spin  ,
,  . These particles with “half-integer spin” (i.e. an element of
. These particles with “half-integer spin” (i.e. an element of  ) are called fermions and they follow a different set of statistics (aptly named Fermi Statistics). Fermi attempted to use various statistical results he derived to explain radiation, leading up to Fermi’s Theory of
) are called fermions and they follow a different set of statistics (aptly named Fermi Statistics). Fermi attempted to use various statistical results he derived to explain radiation, leading up to Fermi’s Theory of  Decay . As it turned out, while this theory was a step in the right direction (it described interactions between particles albeit without specifying how the particles interact) it gave way to the electroweak theory of 1968 (Glashow, Weinberg, Salam) which used the concept of a mediating Boson (namely the
Decay . As it turned out, while this theory was a step in the right direction (it described interactions between particles albeit without specifying how the particles interact) it gave way to the electroweak theory of 1968 (Glashow, Weinberg, Salam) which used the concept of a mediating Boson (namely the  Bosons) which fixed a specific gauge. If you have heard that the gauge group of the standard model of particle physics is
Bosons) which fixed a specific gauge. If you have heard that the gauge group of the standard model of particle physics is  , then the electroweak interaction describes the
, then the electroweak interaction describes the  portion of the gauge group. This implies that
portion of the gauge group. This implies that  plays two roles, for it is also the gauge group of EMF interactions.
plays two roles, for it is also the gauge group of EMF interactions.
 Strong Nuclear Force
Strong Nuclear Force
Until the apex of the
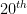
century, many discoveries in physics arose from unexplained experiment that requires theory. The Strong Nuclear Force (SNF) is generally considered to be the last big discovery of this type. Now let’s start in the year 1970. At this time, the existence of smaller particles that made up the protons and neutrons in the nucleus was well-known with the discovery of the quark
(1968, Stanford) and the mystery of beta decay and atomic-level radioactivity was esoteric-no-more after the 1968 introduction of the electroweak interaction. However, the mystery of why these particles “stuck” together and created the coherent object of a proton was still unsolved. The quantum field theory called
Quantum Chromodynamics was invented at this time to describe this mysterious force and how quarks and be put together to make
hadrons.. Without going into details (for I know very few!), one can look at the gluon as an example of a particle involved in mediating the SNF. Essentially, the gluon allows quarks to interact and form cohesive units either as triplets or doublets. Thus the SNF can be thought of as the interaction that keeps hadrons (such as the proton) cohesive.
Development of the String
In the wake of the success of the electroweak model, theoreticians began to look for ways to describe the strong interaction and the field theoretic interpretation of quarks. As mentioned before, Quantum Chromodynamics became the accepted model (and is currently accepted) in the late-1970s. However, QCD had an initial competitor known as a dual-resonance model, proposed by Gabriele Veneziano in 1968. In the 1960s, theories attempted to use scattering amplitudes to demystify the unexplainable experimental evidence for the SNF. Why is scattering related to the SNF? Since physicists were looking for building blocks of the hadrons, a quick way to break something up into it’s component pieces is to break it. It may be easier to explain this with a gedanken:
Suppose that I have a glass sphere filled with marbles of three different masses. If I roll the sphere into a wall with enough force, the ball will smash releasing the marbles everywhere. Since the marbles are of different masses, how far individual marbles roll and the direction they “scatter” in is in general a function of the (internal and external) forces involved in throwing the sphere into the wall. This means that the mass of the marble plays an important role in it’s trajectory and distance travelled.
Now suppose that we could recover the “type of marble” we randomly pick up off the ground based on how far the marbles travelled, the path taken (trajectory) and the force used to smash the sphere. Then this situation is precisely analogous to how particle accelerators try to detect new particles: they smash hadrons (which are analogous to the entire sphere and marble system, with the glass shell of the ball mediating the interaction between the marbles and the sphere) into each other, hoping to pick out smaller particles (the marbles) using the amplitudes of their constituent wavefunctions (analagous to the “distance” the marble rolls from the point of impact) and possibly trajectory. Thus scattering provides the experimenter with an indirect way of measuring the strength of the SNF, based on the amplitude distribution.
The most important SNF-related theory to come out of the 1960s is the Regge Theory. Let’s start by looking through what is already known: physicists understand how EMF scattering works as an  -valued function of angular momentum in the basic quantum mechanical case (i.e. via the Clebsch-Gordan Coefficients ). What the Regge Theory attempts to do is extend (via analytic continuation) the allowed values of angular momentum (those ever-so familiar
-valued function of angular momentum in the basic quantum mechanical case (i.e. via the Clebsch-Gordan Coefficients ). What the Regge Theory attempts to do is extend (via analytic continuation) the allowed values of angular momentum (those ever-so familiar  quantum numbers that chemists often misinterpret) to any value
quantum numbers that chemists often misinterpret) to any value  . In doing this, we introduce complex energies and an object called the Regge trajectory,
. In doing this, we introduce complex energies and an object called the Regge trajectory,  such that if
such that if  then there exists a bound state with energy, angular momentum
then there exists a bound state with energy, angular momentum  . Moreover the Regge trajectory was implicitly defined to have compact support; this is key to the formulation of the open string. The main implication of the theory is as follows:
. Moreover the Regge trajectory was implicitly defined to have compact support; this is key to the formulation of the open string. The main implication of the theory is as follows:
If we have some scattering reaction 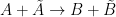 (at energy
(at energy 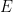 ),where
),where  are the antimatter partners of
are the antimatter partners of  , respectively, then the scattering amplitude
, respectively, then the scattering amplitude  is proportional to
is proportional to 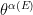 , where
, where 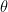 is the scattering angle
is the scattering angle
Note that this claim is testable (we need only to know the energy of the accelerator and 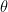 , which is experimentally measurable).
, which is experimentally measurable).
Now back to Veneziano’s contribution: He provided an explicit formulation of scattering amplitudes as the Euler  function and interpreted the evolution of the associated Regge trajectory as a string-like object that represented different particles at different resonances. More precisely, we can explicitly define the Veneziano Scattering Amplitude,
function and interpreted the evolution of the associated Regge trajectory as a string-like object that represented different particles at different resonances. More precisely, we can explicitly define the Veneziano Scattering Amplitude,  in terms of the Mandelstam variables.
in terms of the Mandelstam variables.
Essentially, the Mandelstam variables serve as a way to group together momenta of ingoing and outgoing particles. For example, if we have electron-positron scattering,  then we define the Mandelstam variable
then we define the Mandelstam variable  to be the sum of the momenta of the incoming electron and positron, squared. By conservation of momentum this means that the sum of the momenta of the outgoing electron and positron (squared) is precisely the same. This variable represents the idea that the incoming particles form an intermediate particle that late splits into the outgoing particles.
to be the sum of the momenta of the incoming electron and positron, squared. By conservation of momentum this means that the sum of the momenta of the outgoing electron and positron (squared) is precisely the same. This variable represents the idea that the incoming particles form an intermediate particle that late splits into the outgoing particles.
Next we define the Mandelstam variables  to be the difference in momenta an incoming particle and an outgoing particle. The idea here is that the incoming particle emits an intermediate particle which becomes the outgoing particle. Let’s clear this up, paradoxically, with formality:
to be the difference in momenta an incoming particle and an outgoing particle. The idea here is that the incoming particle emits an intermediate particle which becomes the outgoing particle. Let’s clear this up, paradoxically, with formality:
Suppose we have incoming momenta  and outgoing momenta
and outgoing momenta 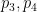 ; then we have the
; then we have the  -channel variable and
-channel variable and  -channel variable,
-channel variable,


Finally we have the Veneziano Scattering Amplitude:

where 
From this equation, we see that we have:
- A linear Regge Trajectory
- A relatively simple amplitude relation that explicitly describes the relationship with the coupling constant

So how do we get from a scattering amplitude to a string? Two words: A Pomeron
In the 1960s and 1970s it was noted that hadron-hadron experiments lead to the following, rather general conclusions (Reference [6]):
- Hadron-Hadron collisions were inelastic and had little or no quantum number flow.
- The forward scattering amplitudes are almost purely imaginary giving credence to the Regge trajectory concept.
- The total likelihood of interaction between particles is asymptotically constant (i.e.
 )
)
As it turns out, a Regge trajectory with  is a sufficient condition for the second and third experimental properties above; any such trajectory is called a pomeron. This trajectory represents a collection of particles and as such it makes predictions of new particles at various
is a sufficient condition for the second and third experimental properties above; any such trajectory is called a pomeron. This trajectory represents a collection of particles and as such it makes predictions of new particles at various  . However, since these particles were not detected in the 1970s, Physicists attempted to use a Kaluza-Klein compactification of Minkowski Space
. However, since these particles were not detected in the 1970s, Physicists attempted to use a Kaluza-Klein compactification of Minkowski Space 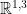 to explain some of the experimental correspondences with the pomeron. The Kaluza-Klein compactifcation starts with
to explain some of the experimental correspondences with the pomeron. The Kaluza-Klein compactifcation starts with  and then mods out by the equivalence relation
and then mods out by the equivalence relation  defined by:
defined by:

for some

, where

is the projection onto the
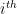
component of

This is simply saying that the extra dimension is compactified into a circle so that we have a cylinder-like space. This effectively says that any “slice” or cross-section is homeomorphic to 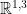 , or
, or  . As it turns out, in this compactification, the interaction of the particles predicted by pomeron is mediated by the release of a cross section of this “cylinder.” This is the first closed string.
. As it turns out, in this compactification, the interaction of the particles predicted by pomeron is mediated by the release of a cross section of this “cylinder.” This is the first closed string.
The evolution of the Regge trajectory could be computed using a construction called the S-matrix that Heisenberg developed in the 1950s as a possible solution to the renormalization problems of pre-Feynman-Schwinger-Tomononga-Dyson quantum field theory. For completeness purposes, it’s probably a good idea to define the S-matrix; I’ll give a little description in the next blog entry that will talk about the construction of the Bosonic string. This novel treatment of a quantum mechanical object as a non-point object grew into string theory as we know it.
Veneziano’s ideas garnered attention from some of the brightest minds of the day, including Y. Nambu (Nobel Prize winner, 2008), D. Gross (Nobel Prize winner, 2004) and the aforementioned Heisenberg. These ideas developed into a few, relatively disconnected string theories. The early string theories were called Bosonic string theories because they could only explain the existence of Bosons (recall: integer spin) and were considered unrealistic because they predicted a particle called the tachyon which necessarily violates special relativity. Another odd flaw with these string theories is that they requires spacetime to actually be of dimension 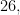 which was portrayed as preposterous at a time when extra-dimensions were looked down upon. In order to describe fermions, early string theorists attempted to add <i>supersymmetry</i> into the theory of the bosonic string. What supersymmetry does is add a relationship between fermionic particles and bosonic particles. How does it do this? Let’s consider the simple example of a graded Hilbert space
which was portrayed as preposterous at a time when extra-dimensions were looked down upon. In order to describe fermions, early string theorists attempted to add <i>supersymmetry</i> into the theory of the bosonic string. What supersymmetry does is add a relationship between fermionic particles and bosonic particles. How does it do this? Let’s consider the simple example of a graded Hilbert space  (one can generalize this to Fock Spaces quite naturally). The idea here is that
(one can generalize this to Fock Spaces quite naturally). The idea here is that 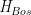 and $\emph{H}_{Ferm}$ each have their own actions
and $\emph{H}_{Ferm}$ each have their own actions  and
and  and as such have their own symmetries. Suppose that these symmetries are two Lie Groups
and as such have their own symmetries. Suppose that these symmetries are two Lie Groups 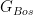 and
and  that have irreducible representations on their respective Hilbert subspaces. Supersymmetry attempts to combine the two Lie groups into a “super Lie group”
that have irreducible representations on their respective Hilbert subspaces. Supersymmetry attempts to combine the two Lie groups into a “super Lie group”  that acts on the entire Hilbert space
that acts on the entire Hilbert space 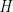 . More concretely (and physically) this says that I can convert a Fermionic symmetry to a Bosonic symmetry if I have actions such that
. More concretely (and physically) this says that I can convert a Fermionic symmetry to a Bosonic symmetry if I have actions such that  induces a conserved current for both Bosonic and Fermionic portions. This is quite unnatural — in fact, the difference in Fermi and Bose statistics ensures that fermions and bosons are treated on equal but separate footings. The hope is that at high energies, such a symmetry becomes apparent and realistic.
induces a conserved current for both Bosonic and Fermionic portions. This is quite unnatural — in fact, the difference in Fermi and Bose statistics ensures that fermions and bosons are treated on equal but separate footings. The hope is that at high energies, such a symmetry becomes apparent and realistic.
Let’s go back to the Bosonic String. Why 26 dimensions? As it turns out, the only way to preserve Lorentz invariance is when the dimension is equal to 26. This is due to the existence of a quantum anomaly. A quantum anomaly is a (natural) physical symmetry that generates a conserved charge in the classical theory but not in the quantum theory. Since the canonical quantization process is somewhat heuristic, one walks in hoping that all of the conserved currents (symmetries) will be preserved upon enforcing commutation relations between annihilation and creation operators. However, as it turns out the only way for there to be a Lorentz Current is if the dimension is 26 (Warning: this is a long computation!). However, if one assumes supersymmetry, it turns out that one only needs 10 dimensions to preserve Lorentz invariance. However it turns out that one loses another symmetry in the process — Chiral symmetry.
Let’s briefly (and superficially) look at the main quantum anomaly that plagued string theory until the introduction of the Green-Schwarz Mechanism in 1984. When one is initially introduced to physics, the notion of right-handed and left-handed coordinate systems is presented intuitively as the naming suggests. However, the choice of the “right-hand rule” is arbitrarily built into mechanics and classical electrodynamics. As it turns out if one doesn’t force a handedness criterion, then it is possible to get some very interesting quantum phenomenon. This choice of “handedness” is known as chirality and it plays an important role in chemistry and physics. In general, it is much easier to formulate a theory with handedness “built-in;” one does this by not specifying an orientation of the cross product. However once experiments dictated that chiral effects are indeed crucial to a full understanding of particle physics, physicists began to incorporate chirality into their equations. One of the greatest triumphs of human intellectualism is the invention of the Dirac Equation. By using a relatively simple mathematical argument, Dirac landed at an equation that described experimental phenomena up to unbelievable accuracy; moreover, it naturally separated chiral solutions. These chiral solutions manifested themselves in the quantum number known as flavor in quantum chromodynamics. The introduction of flavor as a quantum number allowed particle physicists to understand, among other things, that quarks were not all the same. In effect, there are three types of quarks and chirality is the way to separate them experimentally. Let’s just take a look at the Dirac Equation:
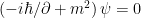
where 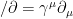 ,
,  is the wavefunction and
is the wavefunction and  is the mass of the particle. Where is chirality defined in this equation? As it turns out the
is the mass of the particle. Where is chirality defined in this equation? As it turns out the  matrices represent the generators of a Clifford algebra. Clifford algebras attempt to generalize the cross and inner products of Euclidean space in order allow both types of handedness.
matrices represent the generators of a Clifford algebra. Clifford algebras attempt to generalize the cross and inner products of Euclidean space in order allow both types of handedness.
To be continued..
, where
is the energy scale (i.e. 1 MeV, 10 GeV, 1 TeV). Note that I’m being a bit sloppy here: The actual scaling is represented by what is known as the
function, which is a function of energy scale. However, the idea is that these contributions are only valid within certain energy regimes (i.e. 1 MeV — 10 TeV). In terms of QCD, one of the biggest problems is elucidating how the strong force works at low energies. The current theory gives a lot of infinite integrals that aren’t renormalizable (the heuristic method that Feynman, et. al came up with removing infinites from expectations of electric or magnetic fields) when the energy is low and this represents a phenomena known as confinement. Effectively, this is a weird quantum mechanical phenomenon that is similar to the fact that you are changing the system by making a measurement. What confinement says is that if you’re at a low enough energy scale (say 1 MeV for protons), you cannot discern quarks from antiquarks because there is not enough energy to break the so-called “Dirac String” connecting the two particles. However, a lot of important quantum mechanical (and even condensed-matter) effects take place around the “condensation” energy (the energy level where confinement occurs for a certain particle). The best attempt to solve this problem is to use something called Lattice Gauge Theory, where you fix a different gauge from the symmetry group of your theory [
for QCD] at each point and use some nearest-neighbor computations. So what does this have to do with having one universal constant?
, where
is the dilaton field [
is the configuration space]. This coupling constant determines the “tension” in a string, just as if one were in classical mechanics. As it turns out, this means that you’ve avoided all the infinities that occur in conventional quantum field theories, because there is a universal coupling constant that doesn’t depend on energy scale. In fact, all of the energy scale dependence is in the fields themselves. This means that a String Theory inherently avoids the somewhat arbitrary algorithms that one follows in Quantum Field Theory to “subtract infinity from infinity.” Think of it as a constructive formulation of a theory from the ground up as opposed to a destructive theory that works from bigger objects down. When you’re trying to “integrate” over a space of bigger objects in a space of lower dimension, you’ll always get an infinity. The converse, however, is similar to the fact that a plane embedded in 3-space has zero volume in 3-space because it’s “width” is zero.
) “requires” 4-dimensions for Lorentz Invariance (3 space, 1 time) and for a string we require 6 extra dimensions to be consistent. In fact the first String Theory (Bosonic String theory) required 26-dimensions, but if one uses supersymmetry you can bring it down to 10-dimensions and include fermions. Just for completeness, let me just explain what supersymmetry is, albeit heuristically. In the real world, we have fermions and bosons and from the Black Body Spectrum and quantum statistical mechanics, we know that they obey different statistical laws. Since statistics are derived from a choice of probability measure on a separable Hilbert Space, this means that we need two Hilbert Spaces, equipped with different integration measures, to accommodate both fermions and bosons. As Dirac realized, fermion expectations rely on anticommutivity of operators whereas bosonic expectations rely on commutivity of operators. This means that our Hilbert Space
should split into the direct sum of two Hilbert Spaces,
. Think of a direct sum as adding the other Hilbert Space’s basis vectors as independent dimensions, just as
is constructed as
, where the first
contributes the
basis vector and the second contributes the
basis vector. Great, but what about relationships between
and
? This is what supersymmetry assumes: There exists an operator
that acts something like the annihilation and creation operators of the harmonic oscillator. This means that I can “trade” a fermion for a boson at some type of energy cost. There is no physical reason for this, but it certainly makes the math a lot easier so physicists took the path of shallowest ascent.
function in non-linear space-times.
![]()

 The idea is that the Euler Characteristic computes something a bit more fundamental about a manifold or topological space that doesn’t change under a broad number of transformations. However this is NOT an analytic piece of information. As it turns out, one need not define a notion of distance in order to compute an Euler Characteristic; in fact, it would make no sense, since a dilation/stretching (of an object endowed with a way to measure distances) is a homeomorphism. Yet the formula
The idea is that the Euler Characteristic computes something a bit more fundamental about a manifold or topological space that doesn’t change under a broad number of transformations. However this is NOT an analytic piece of information. As it turns out, one need not define a notion of distance in order to compute an Euler Characteristic; in fact, it would make no sense, since a dilation/stretching (of an object endowed with a way to measure distances) is a homeomorphism. Yet the formula 
